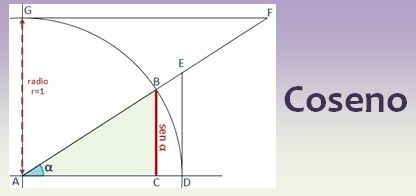
Seno y coseno
Una forma de recordar esta razón junto con las razones de las otras funciones trigonométricas más comunes es con la nemotecnia SOHCAHTOA: SOH = El seno es opuesto sobre la hipotenusa CAH = El coseno es adyacente sobre la hipotenusa TOA = La tangente es opuesta sobre la adyacente Esta razón se puede utilizar para resolver problemas que impliquen distancia o altura, o si se necesita conocer la medida de un ángulo. Ejemplo: ¿Qué es cosΦ?
El coseno es la razón del lado adyacente al ángulo sobre la hipotenusa. cosΦ = 8/17 cosΦ = 0.4706 La función coseno como función periódicaLas funciones trigonométricas se llaman funciones periódicas porque se repiten en un periodo determinado. Observa la gráfica de la función coseno:
Puedes ver que la gráfica se repite a una distancia de 2π. Por tanto, podemos decir que la función coseno tiene un periodo de 2π. Normalmente, cuando se observa la función coseno de esta manera, no se utiliza la medida de grados, sino de radianes. El radián es la unidad estándar de medida de ángulos utilizada en matemáticas. Un círculo completo tiene 2π radianes, que es igual a 360°. El coseno y su relación con un círculo unitarioEn trigonometría, un círculo unitario es un círculo centrado en el origen (0,0) de un plano de coordenadas con un radio de 1.
Coseno complejo
<TR><TD rowspan=”2″ style=”vertical-align:middle”>cos(<I>P</I>°)</TD><TD rowspan=”2″ style=”vertical-align:middle”>=</TD><TD style=”border-bottom: 1px solid black”>5<sup>2</sup> + 8<sup>2</sup> – 7<sup>2</sup></TD><TD rowspan=”2″ style=”vertical-align: bottom; text-align:left”><DIV class=”green”> <I>(evaluate the right-hand side)</I></DIV></TD></TR>
<TR><TD rowspan=”2″></TD><TD rowspan=”2″ style=”vertical-align: middle; text-align:right”>sin(<I>b</I>°)</TD><TD rowspan=”2″ style=”vertical-align:middle”>=</TD><TD style=”border-bottom: 1px solid red”>sin(62°)</TD><TD rowspan=”2″ colspan=”2″ style=”vertical-align:middle; text-align:left”>× 11</TD></TR>
<DIV STYLE=”color:blue;”>If you were happy that the unit worked correctly, please click the button on the right. If you found any problems or would like to add any comments, please fill out the form below and click on the send button.</DIV></TD><TD>
Ley de los cosenos
Las fórmulas del coseno son fórmulas de la función coseno en trigonometría. La función coseno (que se suele denominar “cos”) es una de las 6 funciones trigonométricas que es la relación entre el lado adyacente y la hipotenusa. Existen múltiples fórmulas relacionadas con la función coseno que pueden derivarse de varias identidades y fórmulas trigonométricas. Aprendamos las fórmulas del coseno junto con algunos ejemplos resueltos.
Las fórmulas del coseno hablan de la función coseno (cos). Consideremos un triángulo rectángulo en el que uno de sus ángulos agudos es x. Entonces la fórmula del coseno es, cos x = (lado adyacente) / (hipotenusa), donde “lado adyacente” es el lado adyacente al ángulo x, y “hipotenusa” es el lado más largo (el lado opuesto al ángulo recto) del triángulo. Aparte de esta fórmula general, hay muchas otras fórmulas en trigonometría que definen la función coseno, que puedes ver en la siguiente imagen.
Sabemos que la función coseno (cos) y la función secante (sec) son recíprocas entre sí, es decir, si cos x = a / b, entonces sec x = b / a. Así, la fórmula del coseno utilizando una de las identidades recíprocas es,
Cómo se calcula el seno
La regla del coseno nos dice que cuando tenemos un triángulo rectángulo, coseno=ahcoseno = \frac{a}{h}coseno=ha. La “a” en este caso significa adyacente. La “h” representa la hipotenusa, que se puede encontrar mediante el teorema de Pitágoras. Para encontrar el coseno, todo lo que necesitas es el lado adyacente y la hipotenusa.
Cuando escuchas SohCahToa, no es inmediatamente obvio lo que significa. Pero en realidad es una forma más fácil de recordar cómo usar el seno, el coseno y la tangente que acabamos de aprender. Estas tres son las principales funciones con las que tratarás en los problemas de trigonometría.
Esta tabla ASTC de arriba te ayuda a averiguar qué razón trigonométrica es positiva en cada cuadrante. coscoscos 50° se encuentra en el cuadrante I, donde todas las razones trigonométricas son positivas. coscoscos -50° se encuentra en el cuadrante 4, donde el coseno es positivo. Por eso obtenemos 0,640,640,64 tanto para cos\coscos 50° como para cos\coscos -50°.