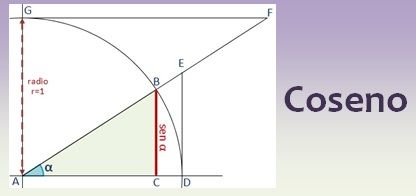
Sin 0
El coseno es una de las principales razones matemáticas trigonométricas. La relación entre las longitudes del lado adyacente al ángulo y la hipotenusa de un triángulo rectángulo se denomina función coseno, que varía al variar el ángulo. Se define en el contexto de un triángulo rectángulo para ángulos agudos. El coseno se utiliza para modelar muchos escenarios de la vida real: ondas de radio, mareas, ondas sonoras, tonos musicales, corrientes eléctricas.
La función coseno se denota simplemente como cos x, donde x es el ángulo. En este artículo, aprenderemos las propiedades básicas del coseno, su gráfica, dominio y rango, derivada, integral y su expansión en serie de potencias del coseno. Cos x es una función periódica y tiene un periodo de 2π.
El coseno o cos x es una función periódica en trigonometría. Consideremos una circunferencia unitaria centrada en el origen del plano de coordenadas. Un punto variable P se mueve en la circunferencia de este círculo. Por la figura, observamos que P está en el primer cuadrante, y OP forma un ángulo agudo de x radianes con el eje x positivo. PQ es la perpendicular caída desde P sobre el eje horizontal. El triángulo se forma, pues, uniendo los puntos O, P y Q como se indica en la figura, donde OQ es la base y PQ la altura del triángulo.
Función senoidal
¿Sabes lo que se dicen dos ángulos que viven dentro del mismo triángulo rectángulo? El primer ángulo dice: “Oye Thelma (¿o es Theta?), no quiero salirme por la tangente, pero ¿cuál es tu seno?”. A lo que el segundo ángulo responde: “Phil (¿o es Phi?), no sé por qué te molestas en preguntar, ¡mi seno es obviamente el mismo que tu coseno!”.
Vale, quizá no sea el mejor chiste del mundo, pero una vez que entiendes los senos y los cosenos, es bastante divertido. Por supuesto, eso significa que si no conoces la diferencia entre un seno y un coseno, actualmente te has quedado fuera en el frío metafórico.
Cuando hablamos del mundo de la trigonometría, aprendimos que la parte de las matemáticas llamada trigonometría se ocupa de los triángulos. Y, en particular, es la parte de las matemáticas que se ocupa de averiguar la relación entre los tres lados y los tres ángulos que componen cada triángulo.
Nos interesa especialmente el tipo especial de triángulos conocido como triángulos rectángulos. Todos los triángulos rectángulos tienen un ángulo de 90 grados (como la esquina de un cuadrado o un rectángulo) y dos ángulos que oscilan entre 0 y 90 grados (como veremos más adelante, la suma de los tres ángulos es de 180 grados).
Sin x/2
El coseno de un ángulo se define como el seno del ángulo complementario. El ángulo complementario es igual al ángulo dado restado de un ángulo recto, 90°. Por ejemplo, si el ángulo es de 30°, su complementario es de 60°. En general, para cualquier ángulo θ,
Como la suma de los ángulos de un triángulo es igual a 180°, y el ángulo C es de 90°, eso significa que los ángulos A y B suman 90°, es decir, son ángulos complementarios. Por lo tanto, el coseno de B es igual al seno de A. Vimos en la última página que sen A era el lado opuesto sobre la hipotenusa, es decir, a/c. Por tanto, cos B es igual a a/c. En otras palabras, el coseno de un ángulo en un triángulo rectángulo es igual al lado adyacente dividido por la hipotenusa:
Pero a2/c2 = (sen A)2, y b2/c2 = (cos A)2. Para reducir el número de paréntesis que hay que escribir, es una convención que la notación sin2 A es una abreviatura de (sin A)2, y de forma similar para las potencias de las otras funciones trigonométricas. Así, hemos demostrado que
cuando A es un ángulo agudo. Todavía no hemos visto cuáles deben ser los senos y cosenos de otros ángulos, pero cuando lo hagamos, tendremos para cualquier ángulo θ una de las identidades trigonométricas más importantes, la identidad pitagórica para senos y cosenos:
Seno y coseno
La regla del coseno nos dice que cuando tenemos un triángulo rectángulo, coseno=ahcoseno = \frac{a}{h}coseno=ha. La “a” en este caso significa adyacente. La “h” representa la hipotenusa, que se puede encontrar mediante el teorema de Pitágoras. Para encontrar el coseno, todo lo que necesitas es el lado adyacente y la hipotenusa.
Cuando escuchas SohCahToa, no es inmediatamente obvio lo que significa. Pero en realidad es una forma más fácil de recordar cómo usar el seno, el coseno y la tangente que acabamos de aprender. Estas tres son las principales funciones con las que tratarás en los problemas de trigonometría.
Esta tabla ASTC de arriba te ayuda a averiguar qué razón trigonométrica es positiva en cada cuadrante. coscoscos 50° se encuentra en el cuadrante I, donde todas las razones trigonométricas son positivas. coscoscos -50° se encuentra en el cuadrante 4, donde el coseno es positivo. Por eso obtenemos 0,640,640,64 tanto para cos\coscos 50° como para cos\coscos -50°.